Bayes Teoremi

Olasılık teorileri arasında en popüler ve yaygın kullanılan teoridir. Olasılıkla ilgili daha önceden bilgi sahibi değilseniz olasılık yazımda bu konuyla ilgili temel kuralları açıklamaya çalıştım o yazıyı da okumanızı öneririm.

Bayes teoremi, 18. yüzyıl İngiliz matematikçisi Thomas Bayes’in adını verdiği koşullu olasılığı belirlemek için kullanılan matematiksel bir formüldür.

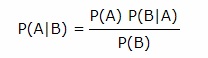
P(A|B) = B olayı gerçekleştiğinde A olayının gerçekleşme olasılığı
P(A) = A olayının gerçekleşme olasılığı
P(B|A) = A olayı gerçekleştiğinde B olayının gerçekleşme olasılığı
P(B) = B olayının gerçekleşme olasılığı

Şimdi bu formülün nasıl çıkarıldığına bakalım. Koşullu olasılık kuralını kullanacağız. Buna göre:

P(A|B) = P(A ve B) / P(B)

Formülünü kullanıyorduk. Aynı şekilde :

P(B|A) = P(B ve A) / P(A)

P(A ve B) = P(B ve A)

Yukarıdaki iki denklemi birleştirirsek.

P(A|B).P(B)=P(B|A).P(A) buradan Bayes kuralını çıkarabiliriz.

P(A|B) = P(B|A) . P(A) / P(B)

Şimdi bu kuralı kullanarak bazı örnekler yapalım.

Örnek: Bir araştırmaya göre her 43 çocuktan 1 tanesi, yetişkinlikte ortaya çıkan belli bir hastalığa yakalanmakta ve tam güvenilir olmamasına rağmen yapılan test sonuçlarına göre, hastalıklı bir çocuğun testi %80 pozitif, sağlıklı bir çocuğun testi ise %10 pozitif sonuç vermektedir. Bu bilgilere göre test sonucu pozitif olan bir çocuğun gerçekten hasta olma olasılığı nedir?

P(A) : Çocuğun hasta olması olasılığı = 1/43
P(B) : Testin pozitif çıkması olasılığı = 1/43 * 0.80 + 42/43 * 0.10 = 5/43
P(A|B) : Pozitif çıkan testin hastalık çıkma olasılığı ( sorulan bu )
P(B|A) : Hastalıklı çocuğun testinin pozitif çıkma olasılığı = 0.80

P(A|B)=P(B|A)*P(A)/P(B) => (0.80 * 1/43) / (5/43) = 0.16 = %16 bulunur.

Örnek: Ali kaşındığını söylüyor. Kedi alerjisi için bir test var, ancak bu test her zaman doğru değil: Gerçekten alerjisi olan insanlar için, testin “Evet” sonucu vermesi %80 oranında. Alerjisi olmayan insanlar için, testin “Evet” sonucu vermesi %10 oranında (“false positive “). Nüfusun %1’inde alerji varsa ve test “Evet” çıkıyorsa, Ali’nin gerçekten alerji olma olasılığı nedir?

A: Alerji, B: Testin Evet çıkması
P(A) : Alerji olasılığı = 0.01
P(B) : Testin evet çıkma olasılığı = ? (hesaplamamız gerekecek)
P(A|B) : Testin evet çıkması durumunda alerji olasılığı = ?? (istenen sonuç)
P(B|A) : Alerji olması durumunda testin evet çıkma olasılığı = 0.80

Önce P(B) yi bulalım. Testin evet çıkma olasılığını alerjisi olan ve olmayanlar için yani tüm nüfus için hesaplayacağız.

P(B) = 0.01 * 0.80 + 0.99 * 0.10 = 0.107 bulduk.

Şimdi bulunacak bir sonuç kaldı tüm verileri denkleme yerleştirip sonucu alalım.

P(A|B)=P(A)*P(B|A)/P(B) => 0.01 * 0.80 / 0.107 = 0.075 => yaklaşık %7 bulunur.

Özel Versiyon Formülasyonu

Şimdi bu teoriyi birden çok olay için genişletelim. Bir B olayının birbiriyle ayrık A olaylarından(A1,A2,A3,…,An) biriyle birlikte gerçekleşebileceğini varsayalım, bu durumda Bayes denklemi aşağıdaki gibi yazılabilir:

P(Ax|B) = P(Ax ve B) / ( P(A1 ve B) + P(A2 ve B)+ ..... P(An ve B) )

Tam burada çarpma kuralını kullanıp teoriyi yeniden yazacağız. Çarpma kuralını hatırlayalım.

Çarpma Kuralı : P(A ve B)= P(A) P(B|A)

Çarpma kuralını uyguladığımızda formülümüz:

Son görünümüne ulaşmış olur. Özel durumları içeren genişletilmiş formülümüzü bir örnekle daha basit ve anlaşılır ifade edersek; Diyelim ki iki ayrık A1 ve A2 olaylarımız var ve Bayes formülünü bunları hesaplayacak biçimde özelleştirelim:

Peki elimizdeki A olaylarından bir tane olduğunu yani ilk durumdaki Bayes formülüne uygun sade bir yapı olduğu durumlarda nasıl bir formül görünümü oluşur? Bu durumda A1 ve A2 => A ve A’ olarak düzenlenir. (A’ anlam olarak A olayının tersini yani değilini ifade eder). Formülü tekrar yazarsak:

P(A|B)=P(A) P(B|A) / ( P(A) P(B|A) + P(A’) P(B|A’) )

Olarak elde ederiz.

Şimdilik bu yazıya burada son veriyorum. Umarım buraya kadar özetlemeye çalıştığım konular bir fikir verebilmiştir.

enginunal.github.io

Engin's Blog

Bayes Teoremi

Özel Versiyon Formülasyonu